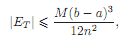CALCULO INTEGRAL: febrero 2012

jueves, 9 de febrero de 2012

VÍDEOS

MÉTODOS DE INTEGRACIÓN

Integración por Partes

Método de sustitución

Integral por sustitución trigonométrica

SUMAS DE RIEMANN

INTEGRAL DEFINIDA

ÁREA DE LA REGIÓN PLANA UTILIZANDO LA INTEGRAL DEFINIDA

LIBROS

1. Introducción al Calculo Integral
http://www.matematicasbachiller.com/temario/calculin/index.html

2. Calculo Integral
http://www.matematicasbachiller.com/videos/calculo-integral

3. Calculo Diferencial en Integral - Serie Schaum - Frank Ayres Jr.

http://libreria-universitaria.blogspot.com/2011/07/calculo-diferencial-e-integral-serie.html

4. Calculo Diferencial e Integral - Piskunov

http://elblogerperu.blogspot.com/2011/02/calculo-diferencial-e-integral-piskunov.html

5. Análisis Matemático

http://www.librosaulamagna.com/libro/ANALISIS-MATEMATICO/528446/7043

6. Elementos Del Calculo Integral

http://www.libreria-limusa-wiley.com/home/product/97/288/elementos-de-calculo-integral

7. Calculo integral - René Jimenes

http://libros.elmundo.es/CALCULO-INTEGRAL-RENE-JIMENEZ-PEARSON--MEXICO--LibroEbook-es-9786074429909.html

OBJETIVOS

GENERAL

1. El objetivo fundamental de crear este blog es afianzar y reforzar los conocimientos básicos y algunos avanzados referentes al calculo integral.

ESPECÍFICOS

2. Dar a conocer el plan de estudio que se está llevando a cabo en el área.

3. No perder contacto con la temática inicial para facilitar el progreso lineal en el aprendizaje.

sábado, 4 de febrero de 2012

REGLA DEL PUNTO MEDIO

Sea f una función continua en [a, b]. La regla del punto medio para aproximar su integral viene dada por:

donde x i es el punto medio del i-ésimo subintervalo [x i-1, x i], es decir, x i = 1/2(x i-1, x i)

Ejemplo. Utilizar la regla del punto medio para aproximar e^(x^2) en el intervalo [0, 1] y en 4 partes iguales.

ESTIMACIÓN DE ERRORES

Cuando se trabaja con aproximaciones es importante conocer con que precisión estamos calculando el valor de la integral. Ademas, es posible que algún método sea sensiblemente mejor que los demás, si bien puede que sea bajo ciertas hipótesis. A continuación enunciamos los errores que se cometen en las reglas de aproximación mas usuales.

1. Si f tiene derivada continua en (a,b) entonces el error Em cometido al aproximar esta integral por la regla del punto medio es

siendo M una cota superior para |f"|, es decir, |f"(x)|≤ M para todo valor de x.

2. si f tiene derivada segunda continua en (a,b), entonces el error Et cometido al aproximar la integral por la regla del trapecio es

3. si f tiene derivada cuarta continua en (a,b), entonces el error Es cometido al aproximar la integral por la regla de simpson es

siendo M una cota superior para | f ^ 4|, es decir, | f ^ 4 (X) | ≤ para todo valor de x.

MÉTODO DE SIMPSON

En este procedimiento, se toma el intervalo de anchura 2h , comprendido entre x i y x i+2 , y se sustituye la función f(x) por la parábola que pasa por tres puntos (x i , y i ) , (x i+1 , y i+1 ) , y (x i+2 , y i+2 ) .

El valor del área aproximada, sombreada en la figura, se calcula con un poco más de trabajo y el resultado es:

La simple inspección visual de esta figura y la que describe el procedimiento de los trapecios nos confirma que el método de Simpson deberá ser mucho más exacto que el procedimiento del trapecio.

El área aproximada en el intervalo [a, b] es:

bien, agrupando términos:

El primer paréntesis, contiene la suma de los extremos, el segundo, la suma de los términos de índice impar, y el tercero la suma de los términos de índice par. En el método de Simpson, el número de divisiones n debe de ser par. En el caso de que el usuario introduzca un número impar el programa lo convierte en el número par siguiente.

Ejemplo. Utiliza la regla de Simpson para aproximar √(1+x^3) con n=4.

MÉTODO DE LOS TRAPECIOS

El método de los trapecios es muy simple y se puede explicar fácilmente a partir de la figra mostrada. Lo importante es recordar la formación de un trapecio como figura geométrica.

Eligiendo un espaciado, cualquiera, para nuestro caso:

se divide el intervalo [a, b] por medio de puntos igualmente espaciados

tenemos que, las ordenadas de dichos puntos son

En cada intervalo (x i , x i+1 ) se sustituye la función f(x) por la recta que une los puntos (x i , y i ) y (x i+1 , y i+1 ) tal como se aprecia en la figura.

La parte sombreada, un trapecio, se toma como el área aproximada, su valor se puede calcular fácilmente

El el área total aproximada es la suma de las áreas de los n pequeños trapecios de anchura h

o bien, agrupando términos

Cuanto mayor sea el número de divisiones del intervalo [a, b] que hagamos, menor será h , y más nos aproximaremos al valor exacto de la integral. Sin embargo, no podremos disminuir h tanto como queramos, ya que el computador maneja números de precisión limitada.

Ejemplo.

Calcular usando la regla del trapecio con n=6.

Δx = (b-a)/n = 3-0/6 = 1/2, luego (b-a)/2n = 1/4

sustituyendo en la fórmula:

= 1/4 [f(xo) + 2f(x1) + 2f(x2) + 2F(x3) + 2f(x4) + 2f(x5) + f(x6)

= 1/4 [f(0) + 2f(1/2) + 2f(1) + 2f(3/2) + 2f(2) + 2f(5/2) + f(3)]

= 1/4 [0.0625 + 0.1230 + 0.1176 + 0.1096 + 0.1 + 0.09 + 0.04]

= 1/4 [0.6427] = 0.1607

PROPIEDADES FUNDAMENTALES INTEGRAL DEFINIDA

Para facilitar el calculo de una integral definida se usan las siguientes propiedades:

1. Si a>b, entonces

2. Si f(a) existe, entonces

3. Si k es una constante cualquiera, entonces

4. Si una función f es integrable en [a, b] y k es una constante arbitraria, entonces

5. Si las funciones f y g son integrables en [a, b] entones f ± g también es integrable en [a, b]

6. Si f es integrables en [a, b], [a, c] y [c, b], y a<c<b, entonces

7. Si f es integrable en un intervalo cerrado I y {a, b, c} I, entonces

8. Si f es integrable en un intervalo [a, b] y f(x) ≥ 0 ∀ x ∈ [a, b], entonces

9. si las funciones f y g son integrables en [a, b], y f(x) ≥ g(x) ∀ x ∈ [a, b], entonces

Ejemplo 1.

Ejemplo 2.

Ejemplo 3.

INTEGRAL DEFINIDA

Definición: La integral definida es un concepto utilizado para determinar el valor de las áreas limitadas por curvas y rectas. Dado el intervalo [a, b] en el que para cada uno de sus puntos x, se define una función f(x) que es mayor o igual que 0 en [a, b], se llama integral definida de la función entre los puntos a y b al área de porción del plano que esta limitada por la función, el eje horizontal OX y las rectas verticales de ecuaciones x=a y x=b.

Teorema fundamental:

La integral definida de f(x) (donde f>0) de a en b es denotada por: